Percentil je míra polohy, který dělí uspořádaný soubor hodnot na 100 stejně velkých částí. Standardně ukazuje celočíselný podíl (procento) pozorovaní v datové sadě pod určitou hodnotou.
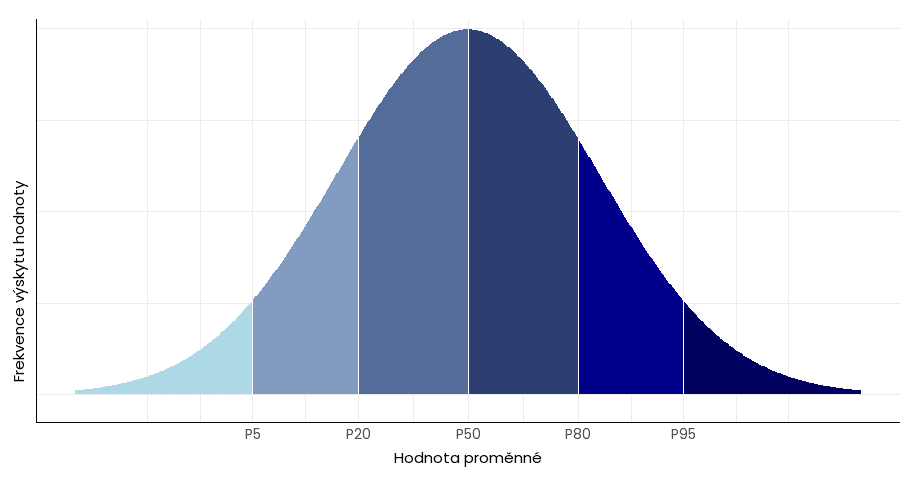
Např. 20. percentil (označovaný jako P20) je hodnota, pod kterou leží 20 % všech pozorování a 80. percentil (P80) je hodnota, pod kterou leží 80 % všech pozorování.
Spolu s dalšími kvantily lze percentil spočítat u ordinálních proměnných a kvantitativních proměnných. U druhé skupiny je výpočet možný za předpokladu rovnoměrného rozložení dat a dostatečného počtu pozorování v každé kategorii (např. u školních známek, kde předpokládáme stejný rozdíl mezi jednotlivými stupni známkování).
Percentil se počítá podle následujícího vzorce (viz příklad níže):
\(P_k \) označuje pořadí hodnoty k-tého percentilu v souboru vzestupně seřazených dat. \(n \) je počet hodnot v datovém souboru. V praxi se percentily počítáme s pomocí statistických programů.
V případě, že výsledkem není celé číslo, je potřeba výsledek upravit lineární interpolací mezi dvěma sousedními hodnotami v uspořádaném datovém souboru. Její vzorec je následující (viz příklad níže):

Zakupte si balíček 2 nebo více vybraných kurzů a ušetřete
\( x_1 \) a \( x_2 \) je menší, resp. větší pořadí hodnoty, pro které provádíme interpolaci. \( y_1 \) a \( y_2 \) je pak menší, resp. větší hodnota, které interpolujeme.
Pozor – aplikace pro statistickou analýzu, jako je Excel a jazyk R, nevyužívají pro získání výsledku lineární interpolaci, ale složitější postupy. Výsledky se proto mohou od ručního výpočtu lišit.
Využití percentilů
Percentily jsou dalším z nástrojů pro popis rozložení dat u velkých datových souborů. U normálního rozložení jsou rozestupy mezi percentily od středu podobné (graf výše), zatímco v souborech se zešikmenými daty (viz míry tvaru) se zpravidla výrazně liší – data se koncentrují na jedné straně rozložení:

Spolu s mezikvartilovým rozpětím a dalšími metodami lze percentily použít pro identifikaci odlehlých hodnot. Za extrémní se mohou považovat hodnoty, které leží pod hranicí 5. percentilu (resp. 1. percentilu) a nad hranicí 95. percentilu (resp. 99. percentilu).
Záleží na kontextu – u dat s pravostranným rozložením lze za extrémní brát hodnoty nad 95. percentilem, protože většina dat se nachází napravo od mediánu. Naopak u normálního rozložení je za odlehlé možné považovat hodnoty pod 5. a nad 95. percentilem.
Percentily jsou dobrým ukazatelem pro srovnávání různých datových sad. Předpokladem je:
- podobné rozdělení (distribuce) datových sad,
- měření na stejné nebo srovnatelné škále,
- dostatečná velikost vzorku (za účelem reprezentace dané populace).
Používají se např. pro porovnání znalostí studentů v různých státech nebo míry znečištění v různých regionech. Ve zdravotnictví a dalších oborech slouží percentily pro stanovení norem:
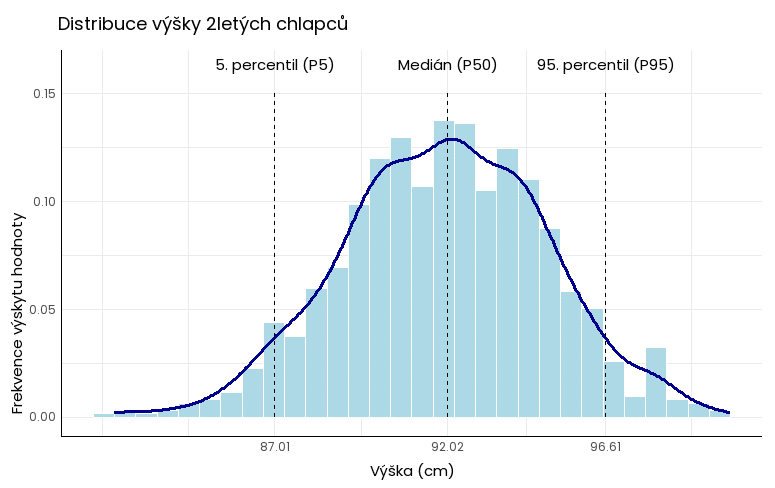
Použití percentilů není vhodné pro:
- malé datové sady (méně než několik desítek hodnot),
- výrazně odlišná distribuce srovnávaných datových sad (např. sada hodnot s normálním rozdělením a sada hodnot s výrazně levostrannou distribucí),
- pro datové sady s vysokým počtem odlehlých hodnot.
Příklad výpočtu percentilů
Vaším úkolem je spočítat 20. a 80. percentil výšky tříletých dívek z následujících dat: 90, 95, 88, 92, 89, 94, 97, 86, 99, 85, 93, 96, 100, 91, 87, 98, 94, 92 a 90 cm. (Jde o ilustrační příklad – pro takto malou datovou sadou není vhodné percentil používat.)
Hodnoty nejprve vzestupně seřadíme:
| Pořadí hodnoty | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Výška (cm) | 85 | 86 | 87 | 88 | 89 | 90 | 90 | 91 | 92 | 92 |
| Pořadí hodnoty | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | |
| Výška (cm) | 93 | 94 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Pro výpočet 20. percentilu z 19 hodnot dosadíme příslušné hodnoty do výše uvedené rovnice:
20. percentil (P20) odpovídá v této sadě 4. hodnotě, tedy výšce 88 cm. V dané datové sadě je tedy 20 % dívek vysokých 88 cm (nebo menších).
Stejným způsobem spočítáme i 80. percentil:
80. percentil (P80) odpovídá 16. hodnotě, výšce 97 cm. V dané sadě dosahuje 80 % dívek výšky maximálně 97 cm.
Příklad výpočtu percentilů s lineární interpolací
Vyjdeme ze stejných dat jako v předchozím příkladu, přidáme pouze navíc jednu hodnotu (106 cm). V datovém souboru bude tedy 20 hodnot:
| Pořadí hodnoty | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Výška (cm) | 85 | 86 | 87 | 88 | 89 | 90 | 90 | 91 | 92 | 92 |
| Pořadí hodnoty | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Výška (cm) | 93 | 94 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 106 |
Hodnoty dosadíme do vzorce pro výpočet 20. percentilu:
Pořadí číslo 4,2 (\( x \)) neexistuje. Provedeme proto lineární interpolaci mezi hodnotami na 4. a 5. místě (\( x_1 \) a \( x_2 \)). Tyto hodnoty (88 a 89 cm, tedy \( y_1 \) a \( y_2 \)) dosadíme do příslušného vzorce (viz výše):
Hodnota 20. percentilu se tedy rovná 88,2 cm. Stejným postupem získáme u 80. percentilu k (neexistujícímu) pořadí 16,8. Po použití lineární interpolace nám vyjde hodnota 80. percentilu 97,8 cm.
Výpočet percentilů v Excelu
# buňky A1 až A100 obsahují naměřené hodnoty
# funkce pro výpočet percentilů
=PERCENTILE.INC(A1:A100, 0.05) # pro výpočet P5
=PERCENTILE.INC(A1:A100, 0.2) # pro výpočet P20
=PERCENTILE.INC(A1:A100, 0.8) # pro výpočet P80
=PERCENTILE.INC(A1:A100, 0.95) # pro výpočet P95Výpočet percentilů v jazyce R
# naměřené hodnoty
data <- c(3, 5, 6, 7, 8)
# funkce pro výpočet percentilů P5, P20, P80 a P95
quantile(data, probs = c(0.05, 0.2, 0.8, 0.95))
# funkce pro výpočet percentilů P5, P20, P80 a P95 lineární interpolací
quantile(data, probs = c(0.05, 0.2, 0.8, 0.95), type = 6) Poslední místa –
Poslední místa – 


